并查集介绍

发表于 | 分类于

本篇通过讲解一道例题来介绍并查集这种数据结构

什么是并查集?

wiki:
在计算机科学中，并查集是一种 树型 的数据结构，用于处理一些不相交集合的 合并 及 查询 问题。有一个 联合-查找 算法定义了两个用于此数据结构的操作：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。

先上题 HDOJ 1856

拿sample来说

第一个sample：

4
1 2
3 4
5 6
1 6

数据结构变化是怎么样的呢

{1},{2},{3},{4},{5},{6}
->{1,2},{3},{4},{5},{6}
->{1,2},{3,4},{5},{6}
->{1,2},{3,4},{5,6}
->{1,2,5,6},{3,4}
于是元素最多的集合里面有4个元素
输出 4

sample2同理

在上文中提到，并查集包括两种操作 查找 和 合并

怎么实现查找?

并查集是一种树形结构
每一个元素(树节点)都有一个父亲节点(如果节点是单独的 那么它的父亲节点就是它本身)
我们用父亲节点来给集合编号
比如
{1} 的编号是1
{2,3} 的编号是2 (当然你也可以设置为3,这并不影响)
我们用数组来表示某一个节点的父亲节点是什么
比如

1
bin[node]=root;

即node节点的父亲节点是root
在数次合并操作之后(先不管我们是如何合并的 但总有某一个node节点的父亲节点变了)
我们不能保证在同一个集合内的元素都指向了同一个根
比如 集合 {1,2,3}

1
2
3
4
bin[1]=1;
bin[2]=1;
bin[3]=2;
//注意:这里的子节点不能指向自己 否则 这个节点是独立的 这与它是"子节点"这一描述不符

我们知道 一个集合内的所有元素都可以拿来修饰这个集合 这会引起歧义(可能吧)
所以我们查找某个节点是属于哪个集合的时候 不能简单地bin[node]操作
故我们定义find函数:

1
2
3
4
inline int find(int a){
    while(bin[a]!=a) a=bin[a];
    return a;
}

当然也有递归版本

1
2
3
4
inline int find(int a){
    if(bin[a]!=a) return find(bin[a]);
    else return a;
}

怎样实现合并?

好了查找操作介绍完了 然后介绍合并操作
不难想到
如果你要合并集合S,T
只要把集合T的根接到S上面去就行了(把一个集合理解为一棵树)

1
2
3
4
inline void union(int a,int b){
    bin[find(a)]=find(b);
    return;
}

这个时候问题来了
为什么我要把T的根接到S上去呢，为什么不把S的根接到T上去呢
这个时候，就有一个效率的问题 请看图: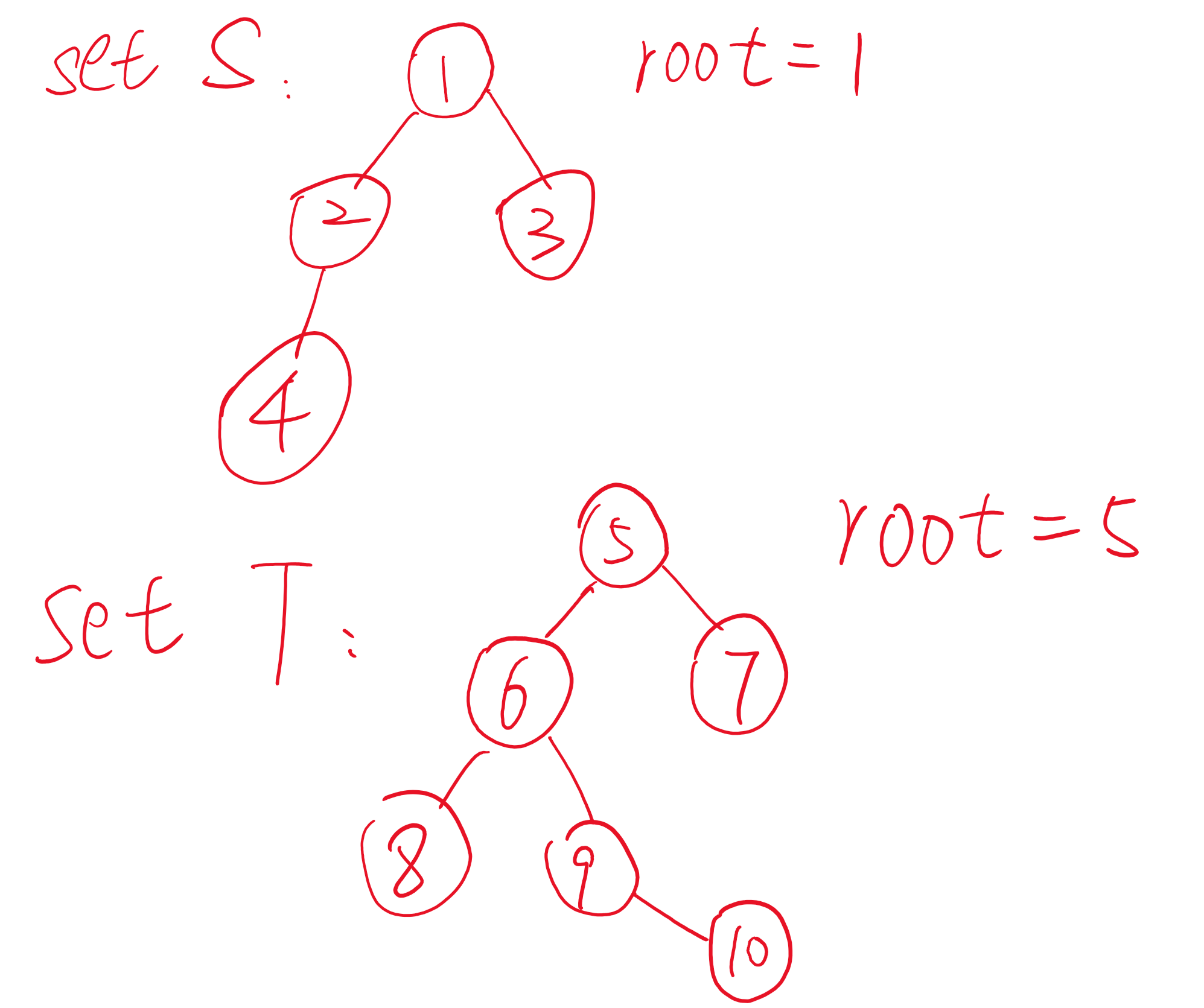
pic1
两棵树S,T
如果我把S接到T上
是这样的: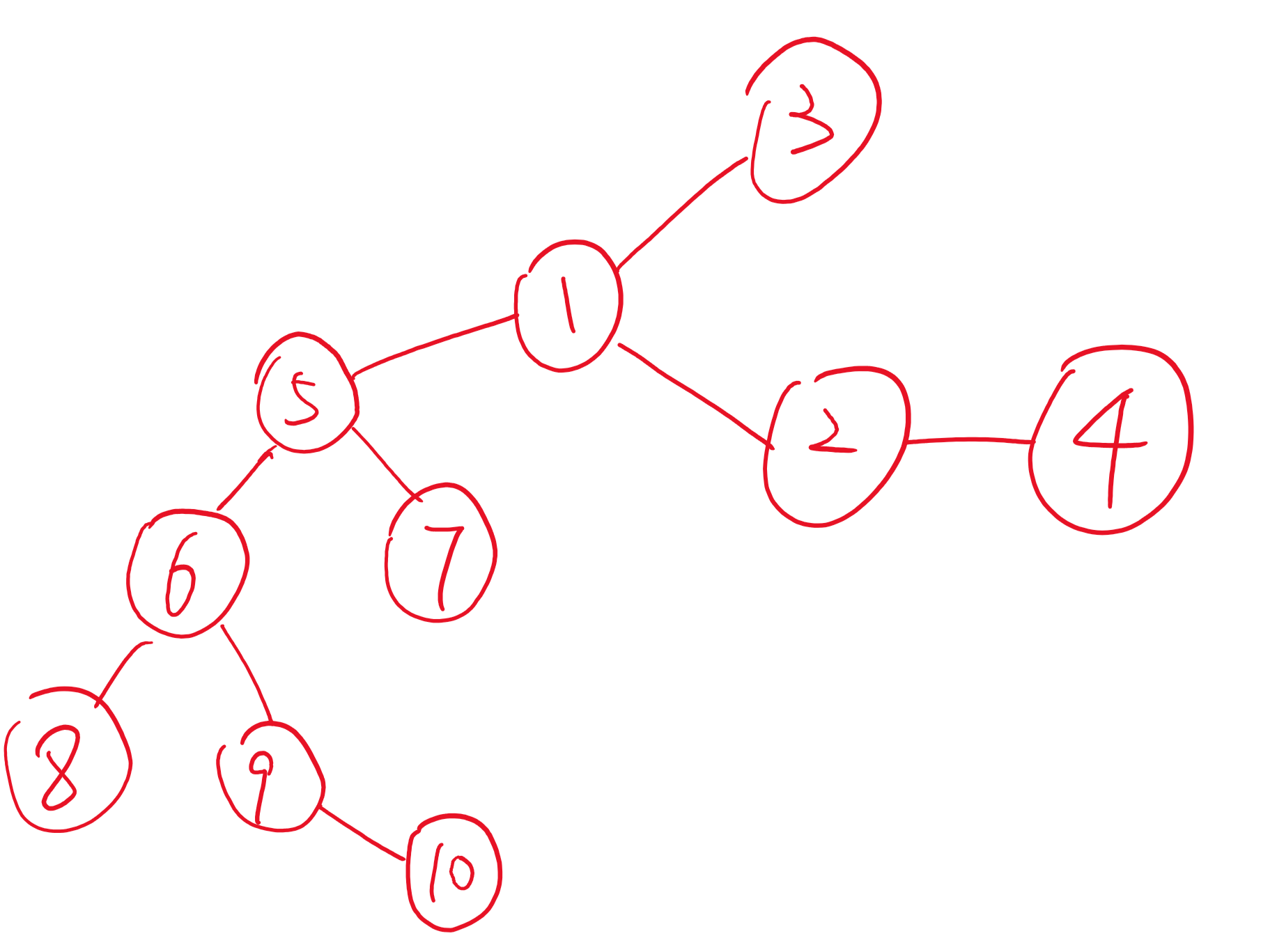
pic2
如果我把T接到S上
是这样的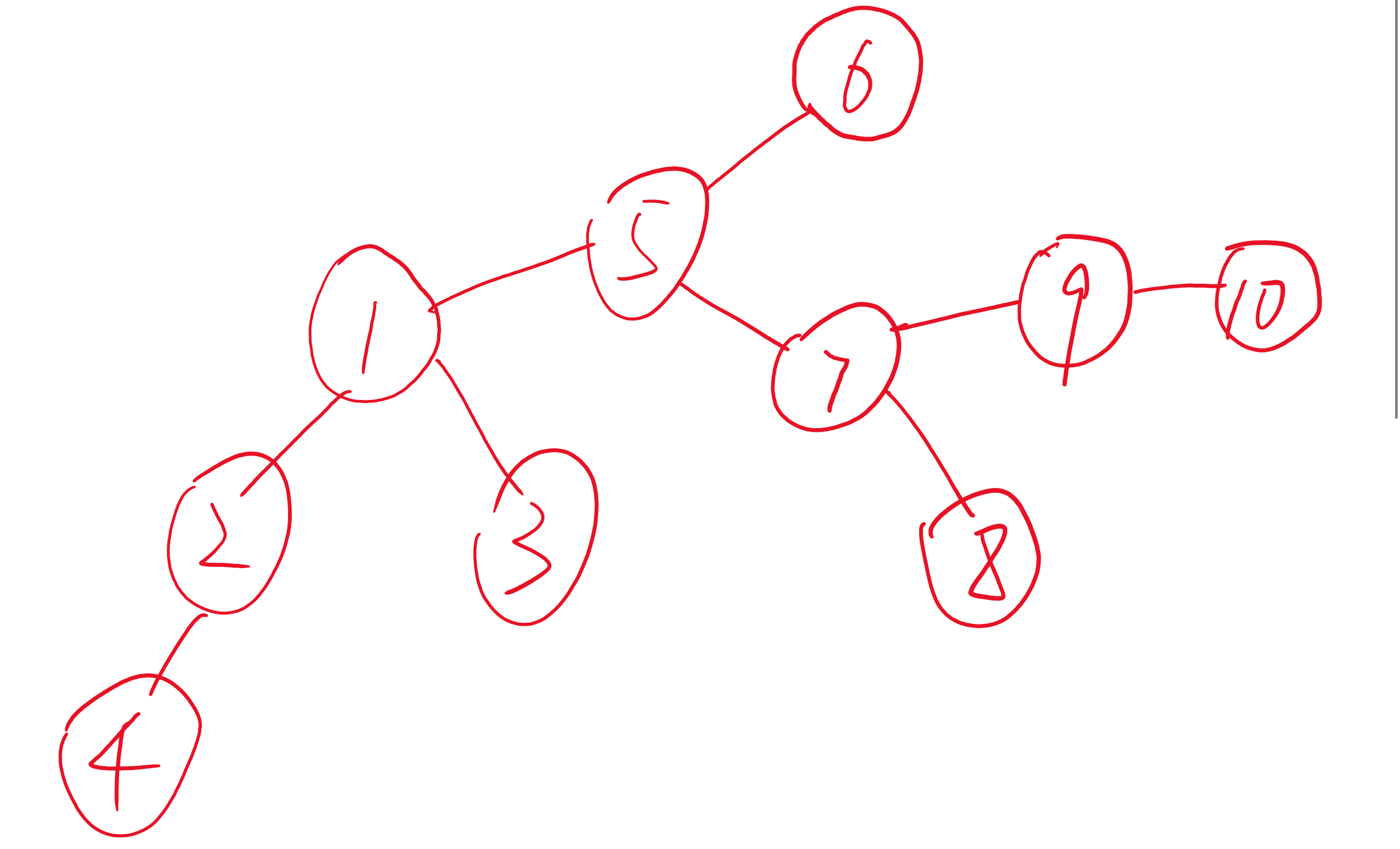
pic3
来观察一下区别
前者，如果我们执行操作find(4)内部我们可能最多要循环3次
后者，如果我们执行操作find(10)内部我们可能最多要循环4次
看出差别了么
那怎么判断我们应该把谁接到谁呢?
别急 先看代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int bin[N],rnk[N];
//initialization
inline void Init(int n){
    for(int i=1;i<=n;i++) {
        bin[i]=i;
        rnk[i]=1;
    }
    return;
}
//find() code
//......
//-----------

inline void union(int a,int b){
    a=find(a);
    b=find(b);
    if(rnk[a]>=rnk[b]){
        bin[b]=a;
        if(rnk[a]==rnk[b]) rnk[a]++;
    }
    else bin[a]=b;
    return;
}

我们引入了rnk数组 这个数组记录了并查集树结构的高度(秩)
这种优化叫做按秩合并
当树S的高度比树T的高度低的时候 把S接到T上去(反之)
这样可以有效减少find()函数的复杂度

好了说了那么多 我们来做一下开头的题目
find()函数没问题了 union()操作介绍完了
现在还有问题?
如果我要知道一个集合有多少元素怎么办？
笨 看看多少节点是同一个根啊
那我要知道有多少集合怎么办?
看有多少节点的父节点指向自己的

话不多说 贴代码了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//C++ code
#include<bits/stdc++.h>

using namespace std;

unordered_map<int,int> bin;
unordered_map<int,int> rnk;
unordered_map<int,int> cnt;

inline int find(int a){
    int tmp=a;
    while(bin[a]!=a) a=bin[a];
    int root=a;
    while(tmp!=bin[tmp]){
        int nx=bin[tmp];
        bin[tmp]=root;
        tmp=nx;
    }
    return a;
}

inline void Union(int a,int b){
	a=find(a);
	b=find(b);
    if(rnk[a]>=rnk[b]){
        bin[b]=a;
        if(rnk[a]==rnk[b]) rnk[a]++;
    }
    else bin[a]=b;
    return;
}

int main(){
    int n;
    while(cin>>n){
        bin.clear();
        rnk.clear();
        cnt.clear();
        for(int i=1;i<=n;i++){
            int a,b;
            scanf("%d%d",&a,&b);
            if(!bin.count(a)) {
                bin[a]=a;
                rnk[a]=1;
            }
            if(!bin.count(b)) {
                bin[b]=b;
                rnk[b]=1;
            }
            Union(a,b);
        }
        if(n==0){
            cout<<1<<endl;
            continue;
        }
        for(std::unordered_map<int,int>::iterator iter=bin.begin();iter!=bin.end();iter++){
            cnt[find(iter->first)]++;
        }
        int maxn=0;
        for(std::unordered_map<int,int>::iterator iter=cnt.begin();iter!=cnt.end();iter++){
            maxn=max(maxn,iter->second);
        }
        cout<<maxn<<endl;
    }
    return 0;
}

ps:我路径压缩的原因是交上去发现TLE了…没想到压缩了路径还是TLE 后来发现一大部分原因是cin太慢了….于是就换了scanf orz

下一讲: 用并查集实现的kruskal算法 用于解决最小生成树问题