本章介绍viterbi算法

markov chain

大坑,在讲viterbi算法之前,先来讲讲markov chain

markov chain(马尔科夫链)
定义：
为状态空间中经过从一个状态到另一个状态的转换的随机过程
性质：
下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关（无记忆性）

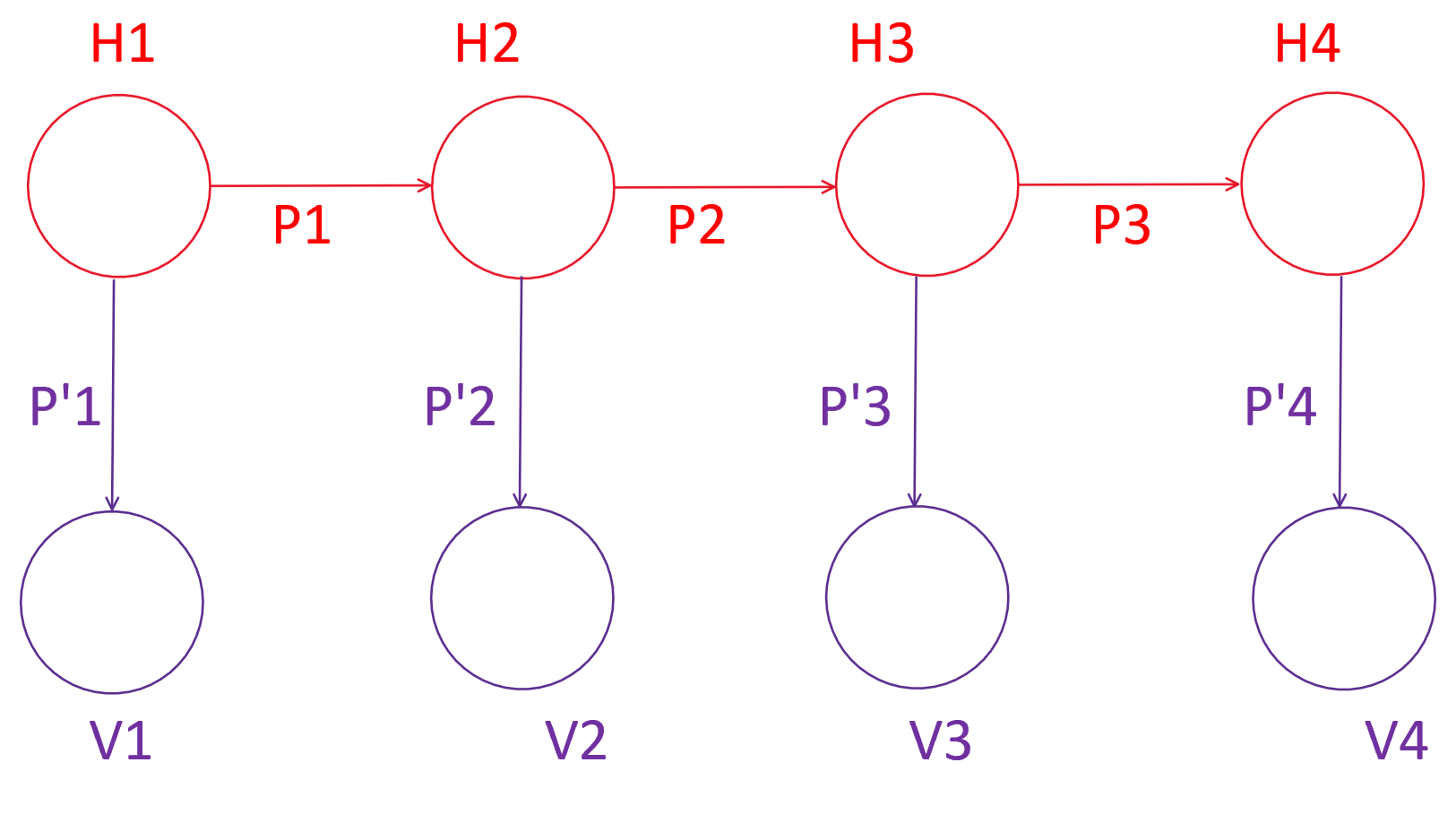
上图的红色部分表示了一条（隐）马尔科夫链
H1,H2,H3,H4表示状态
P1,P2,P3表示一个状态到另一个状态的转换概率

举个例子例子是这样的
HDOJ 4865

题目给出了一个状态机见图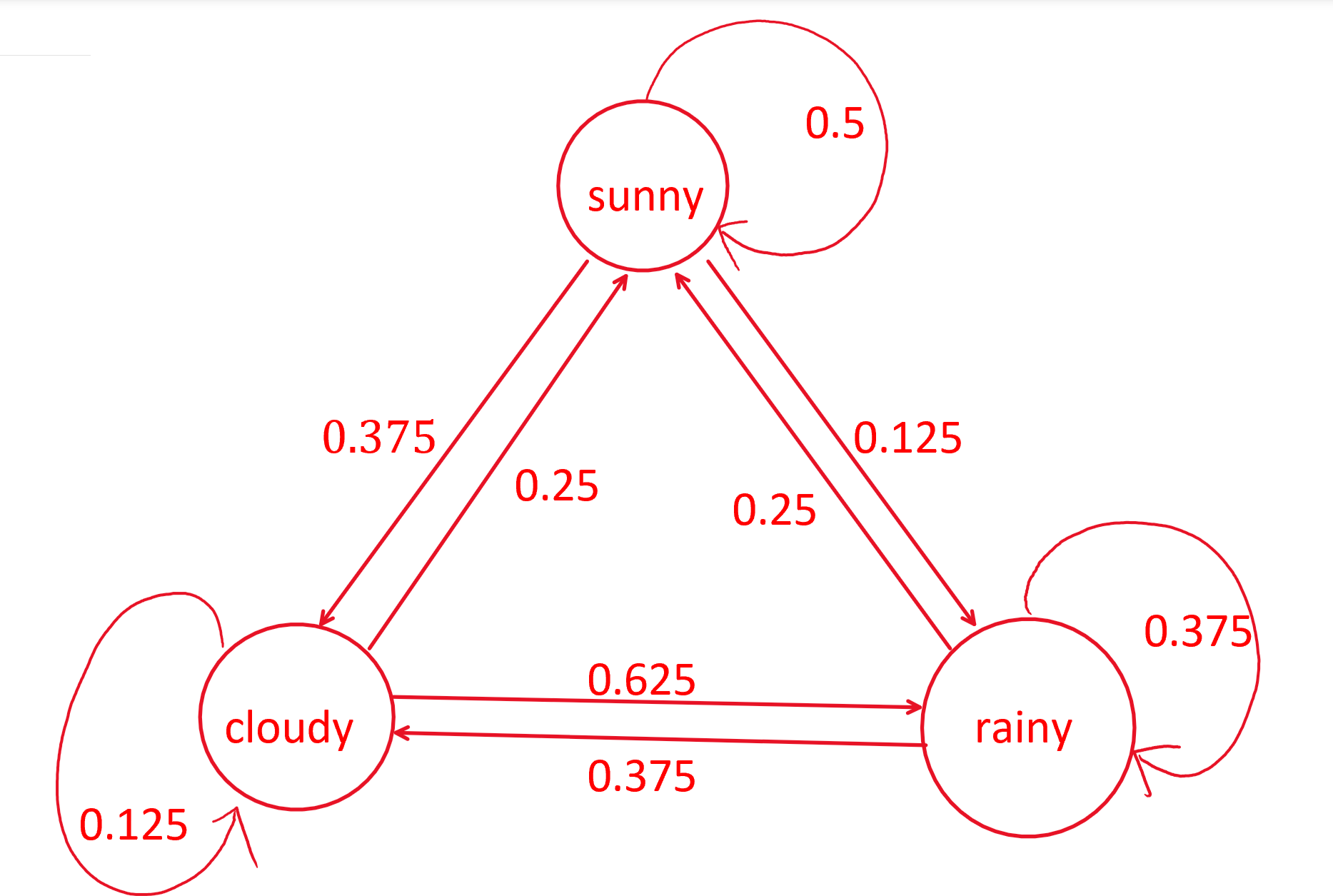

还有一个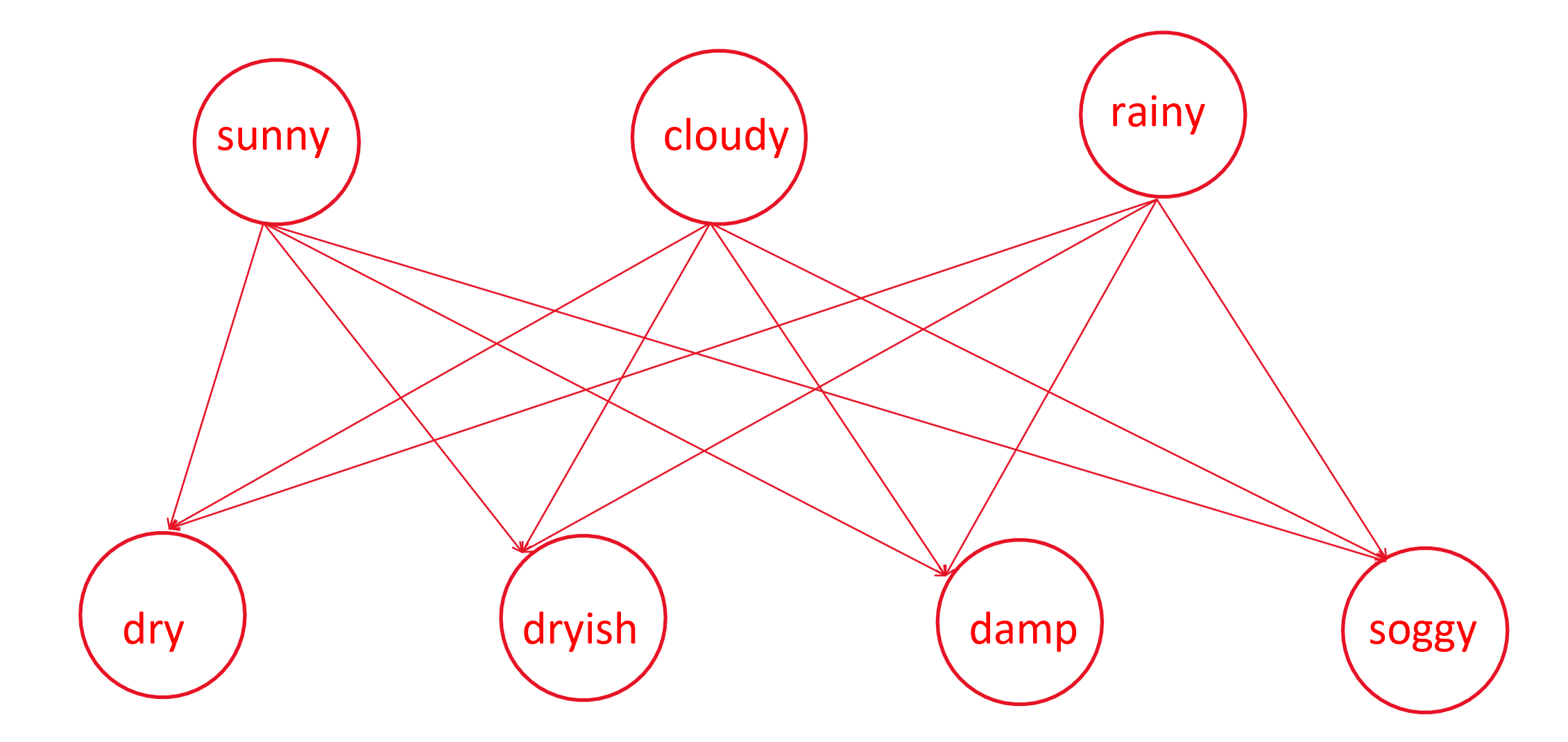

(线太多了就不写概率了)
图1表示从前一天到后一天的天气转移概率
图2表示当天的天气的叶片状态表示概率
题目也给出了第一天的天气初始概率

p[0][sunny]=0.63,p[0][cloudy]=0.17,p[0][rainy]=0.2

和每一天的叶子湿度情况(输入数据)

input[i] (i=0,1,2,…,N-1)

Hidden Markov Model

这是一个简单的隐式马尔科夫模型(HMM)
我们要解决的问题是
第N天最有可能是什么天气并回溯输出1~N天的天气
这是HMM的三个经典问题之一

第K天天气是weather[i]的概率是多少?

第K天最有可能是什么天气?

只给出K天里的叶子湿度情况其他什么都不知道从而建立一个晴雨转换表,和叶片湿度概率表(也就是上面的图1图2)(这个是最复杂的)

三个问题对应的算法分别是

forward/backward algorithm

viterbi algorithm

Baum-Welch algorithm

本篇只讲viterbi,还有两个坑以后再填
也就是例子所要解决的问题之二

viterbi algorithm

数学工具支撑

显然我们需要一个数学模型来描述这些个状态机
矩阵
$$
A=
\left[
\begin{matrix}
0.5 & 0.375 & 0.125\\
0.25 & 0.125 & 0.625\\
0.25 & 0.375 & 0.375
\end{matrix}
\right]
$$
表示天气转移矩阵(transition probability matrix)
A[i][j]表示从i天气转移到j天气的概率
$$
B=
\left[
\begin{matrix}
0.6 & 0.2 & 0.15 & 0.05\\
0.25 & 0.3 & 0.2 & 0.25\\
0.05 & 0.10 & 0.35 & 0.50
\end{matrix}
\right]
$$
表示叶片湿度概率矩阵(emittion probability matrix)
B[i][j]表示i天气下叶片为j湿度的概率

问题分析

viterbi算法其实是一个dp算法
不难发现
假设weather[]是天气数组
如果要求第K天天气为weather[i] 的最大概率
那么可以通过比较K-1天从weather[0],weather[1],weather[2]转移到K天的天气概率,取最大的概率
这是一个重叠的子问题(类似于多阶段决策?)
那么我们先求出第一天最大概率的天气
然后求出第二天第三天…直到第N天
题目给了我们第一天的数据包括天气概率和叶片湿度
那么第一天是
sunny的概率为:0.63 * b[0][input[0]]
cloudy的概率为:0.17 * b[1][input[0]
rainy的概率为:0.2 * b[2][input[0]]
从而求出第二天的概率分布

1 2	dp[1][i]=max(dp[0][k]a[k][i]b[i][input[1]]) i,k=sunny,cloudy,rainy

很容易理解就和最短路floyd算法的路径转移差不多
从前一天的k天气转移到后一天的i天气再转移到后一天的叶片湿度情况然后取最大的那个
如此递推求到N天的概率分布答案就是dp[N][0],dp[N][1],dp[N][2]中最大的
题目还需要打印路径用一个path数组记录即可最后逆向输出用stack还是vector还是裸的数组都没事和viterbi算法本身关系不大
题目差不多讲完了也通过了具体例子来描述viterbi 先给出例子的代码之后我们再来分析一下viterbi算法想要解决的问题和思想以及应用

实现

代码如果没兴趣的话可以跳过不看

//C++ code
#include<bits/stdc++.h>

using namespace std;

const double INF=1e7;
const double a[3][3]={
    {0.5,0.375,0.125},
    {0.25,0.125,0.625},
    {0.25,0.375,0.375}
};//trans matrix

const double b[3][4]={
    {0.6,0.2,0.15,0.05},
    {0.25,0.3,0.2,0.25},
    {0.05,0.10,0.35,0.50}
};//emit matrix

int input[55];//humidity of leaves  input[day]
double dp[55][3];//answers dp[day][weather]
int path[55][3];//print trans matrix  path[day][weather]

inline int index(string a){
    if(a=="Dry") return 0;
    else if(a=="Dryish") return 1;
    else if(a=="Damp") return 2;
    else if(a=="Soggy") return 3;
    return -1;
}

inline string index(int a){
    if(a==0) return "Sunny";
    else if(a==1) return "Cloudy";
    else if(a==2) return "Rainy";
    return nullptr;
}

inline void init(){
    dp[0][0]=log(0.63*b[0][input[0]]);
    dp[0][1]=log(0.17*b[1][input[0]]);
    dp[0][2]=log(0.2*b[2][input[0]]);
    return;
}



int main() {
    // #ifndef ONLINE_JUDGE
    // freopen("input.in","r",stdin);
    // #endif
    // int begin_time=clock();
    int t;
    cin>>t;
    int kase=1;
    while(t--){
        init();
        int n;
        cin>>n;
        for(int i=0;i<n;i++){
            string leaf;
            cin>>leaf;
            input[i]=index(leaf);
        }
        for(int i=1;i<n;i++){
            for(int j=0;j<3;j++){
                dp[i][j]=-INF;
                path[i][j]=-1;
                for(int k=0;k<3;k++){
                    if(dp[i][j]<dp[i-1][k]+log(a[k][j]*b[j][input[i]])){
                        dp[i][j]=dp[i-1][k]+log(a[k][j]*b[j][input[i]]);
                        path[i][j]=k;
                    }
                }
            }
        }
        double maxp=-INF;
        int maxn=-1;
        for(int i=0;i<3;i++){
            if(dp[n-1][i]>maxp){
                maxp=dp[n-1][i];
                maxn=i;
            }
        }
        stack<int> ans;
        ans.push(maxn);
        for(int i=n-1;i>0;i--){
            ans.push(path[i][maxn]);
            maxn=path[i][maxn];
        }
        printf("Case #%d:\n",kase++);
        while(!ans.empty()){
            cout<<index(ans.top())<<endl;
            ans.pop();
        }
    }
    // cout<<"time use: "<<clock()-begin_time<<" ms"<<endl;
    return 0;
}

缺点改进:

viterbi算法在数学逻辑上是没有问题的但是在计算机科学中会有一点问题问题出在概率的计算上面
我们知道计算机在进行浮点运算的时候会有误差(具体可以了解IEEE 754)
特别的是计算机在进行很小的浮点数时候会有明显的下溢
而概率计算中随着马尔科夫链的增长链可能性的增多各个可能性的概率会慢慢下降如果仍然进行乘法运算下溢不可避免从而造成不可避免的误差
所以我们需要想一个办法本篇开头的题目中有一个小小的hint 不知是否注意到

Log is useful.

我们知道 $ \log(a*b)=\log(a)+\log(b) $
并且对于较小的x,log(x)可以起到放大绝对值值的作用
从而避开了概率越算越小的情况

思想

viterbi算法是一个典型的概率dp算法
求解HMM模型可以使用暴力算法不过这样的复杂度是难以忍受的
而通过记录上一个状态的答案求解下一个状态拿空间换时间可以大大减降低复杂度
这也是dp(动态规划)算法的优势所在

review:

最后我们复习一下viterbi算法所要解决的问题
我们通过可以观测的现象,和已知的一些状态转换的概率情况,通过综合状态转换的概率和前一个状态情况来求得下一个状态的情况,也可以记录整条马尔科夫链,并输出.

应用:

HMM是一个模型通过viterbi算法当然我们可以用来解决开篇提到的天气预测问题
也可以解决其他的预测问题和解码问题等